Solución a acertijos matemáticos I

Entrada realizada por Sofía Donoso Gómez

Acertijo nº1:
Hay gatos metidos en un cajón cada gato en un rincón si cada gato ve tres gatos, ¿cuántos gatos son? (cuatro)

Acertijo nº2:
El boticario y su hija, el medico y su mujer, comieron nueve pasteles y solo tocaron a tres, ¿puede ser? (sí por que la hija y la mujer es la misma persona)

Miguel de Guzmán

Una paradoja no es una desgracia, es una gran oportunidad, pues indica que hay algo profundo debajo de todo el asunto que no hemos entendido bien y que nos puede conducir a nuevos mundos.

Miguel de Guzmán

Acertijos matemáticos I

Entrada realizada por Sofía Donoso Gómez

Acertijo nº1:
Hay gatos metidos en un cajón cada gato en un rincón si cada gato ve tres gatos, ¿cuántos gatos son?

Acertijo nº2:
El boticario y su hija, el medico y su mujer, comieron nueve pasteles y solo tocaron a tres, ¿puede ser?


Las respuestas saldrán publicadas dentro de una semana. Espero encontrar muchas soluciones en los comentarios. A ver quién acierta.

UN POCO DE FALSA ESTADÍSTICA

Entrada realizada por Ana López Calero


La estadística, es una parte de las matemáticas que se ocupa de la obtención, organización y análisis de la información numérica. Esta tiene cada vez un papel más importante en la actualidad, ya que constantemente somos bombardeados por datos estadísticos, aunque no todos son completamente ciertos.

Hay muchas personas que (por falta de conocimientos estadísticos) se impresionan muy fácilmente con ciertos datos estadísticos usados de manera errónea, frecuentemente a conciencia, por los medios de comunicación para captar la atención. Aquí podemos encontrar algunos ejemplos interesantes:

-Las estadísticas muestran que casi todos los accidentes de circulación se producen entre vehículos que ruedan a velocidad moderada. Muy pocos ocurren a más de 150 Km. por hora. ¿Significa esto que resulta más seguro conducir a gran velocidad?
No, de ninguna manera. Con frecuencia, las correlaciones estadísticas no reflejan causas y efectos. Casi todo el mundo circula a velocidad moderada, y como es natural, la mayoría de los accidentes se producen a estas velocidades.

-Las estadísticas muestran que la mortalidad por tuberculosis es mayor en Segovia que en las demás provincias, ¿significaría esto que el clima segoviano favorece el contagio tuberculoso?
Todo lo contrario. El clima segoviano es tan beneficioso para los tuberculosos que muchos acuden allí para restablecerse. Naturalmente, ésta es la causa de que aumenten allí los fallecimientos provocados por el mal.

-Un reciente estudio psicopedagógico ha mostrado que los niños de pie grande saben leer mejor que los de pie pequeño. ¿Permitirá el tamaño del pie medir la capacidad de lectura de los niños?
No, desde luego. El estudio se hizo sobre escolares que están en crecimiento. Todo cuanto se demostró en él es que los niños mayorcitos, cuyos pies son más grandes, leen mejor que los pequeñines.

-Suele decirse que casi todos los accidentes de automóvil ocurren cerca de casa. ¿Significa esto que viajar por carretera, a muchos kilómetros de nuestra ciudad, es menos peligroso que callejear por nuestro barrio?
No. Las estadísticas reflejan, sencillamente, que se usa el coche por los alrededores de nuestra residencia que por carreteras alejadas.

-Un estudio demostró que en cierta región las tasas de fallecimiento por cáncer y de consumo de leche eran de las más altas del país. ¿Significa esto que beber leche puede ser causa de cáncer?
No. Resulta que en la zona el clima es benigno y en ella reside gente mayor y acaudalada. Siendo el cáncer aflicción común entre las personas de mayor edad, ésa es la razón del aumento de mortalidad por cáncer.

-Otro estudio mostró que en cierta ciudad se produjo un súbito aumento de mortalidad por fallo cardíaco y un fuerte incremento en el consumo de cerveza. ¿Es posible que beber cerveza sea causa de que aumente la probabilidad de ataque al corazón?
No. En ambos casos el aumento fue debido a un veloz incremento de la población. Por igual causa, los ataques al corazón podrían ser atribuidos a cientos de otras cosas: aumento del consumo de café o de ver la televisión.

-Un estudio hizo ver que en cierta población europea se produjo un fuerte crecimiento de la población y un notable incremento del número de nidos de cigüeñas. ¿No es esto demostración de que son las cigüeñas quiénes traen a los niños al mundo?
No. Refleja el hecho de que al aumentar el número de edificios las cigüeñas dispusieron de más sitios donde anidar. Las parejas recién casadas suelen irse a vivir a casas nuevas, donde no hay nidos de cigüeñas.

-Según las estadísticas los diestros viven más que los zurdos. ¿Será eso cierto?
Las estadísticas demuestran que la mayoría de los zurdos son jóvenes. Pero esto no quiere decir que mueran pronto por ser zurdos. Lo que ocurre es que hace años, en las escuelas se insistía en que los zurdos se acostumbrasen a usar su mano derecha.

De estos ejemplos podemos sacar la conclusión de que quizás debamos leer y observar dos veces las estadísticas que nos encontramos diariamente y ser un poco más críticos con la información que recibimos.No siempre es realmente cierta.A continuación podemos observar como los publicistas utilizan gráficas trucadas para acentuar lo que les beneficia y esconder la realidad, haciéndonos caer en el error.

Como podemos observar en el gráfico ,Fotocasa no pone la escala de medida, no dice qué está midiendo,ninguno de sus gráficos empieza desde cero, sino desde 1.250.000 para ocultar lo pequeña que es la diferencia entre ambas empresas,utiliza la perspectiva para que los datos iniciales parezcan más pequeños y los últimos más grandes y utiliza bloques tridimensionales para mostrar elementos unidimensionales, con lo que consigue un mayor efecto volumen.




Si quieres demostrar algo absurdo toma un montón de datos, tortúralos hasta que digan lo que quieres demostrar, y a la confesión así obtenida llámale "estadística". (Darrel Huff, "How to lie with statistics")

Si se reúnen suficientes datos, se puede demostrar cualquier cosa con ayuda de la estadística. (Ley de Williams y Holland).

Pi, el número.

Casi todo el mundo conoce el número π, pero pocos son los que comrenden verdaderamente la profundidad de este número. El número π es la relación entre las longitudes de una circunferencia y su diámetro, en Geometría euclidiana. Es un número irracional y una de las constantes matemáticas más importantes. Se emplea frecuentemente en matemáticas, física e ingeniería.


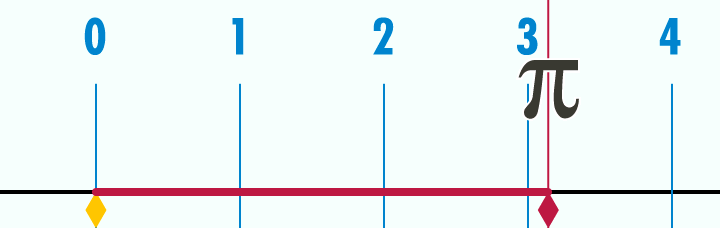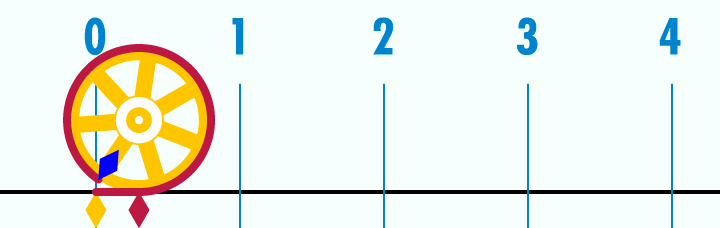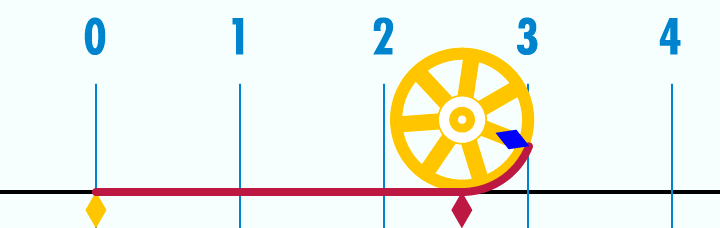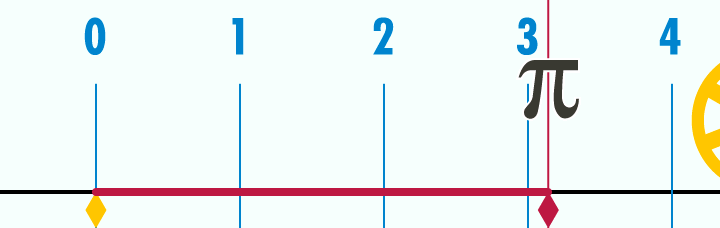
Existen múltiples fracciones que se aproximan al valor de π y que han ido apareciendo a lo largo de la historia para poder hacer cálculo lo más exactos posibles. Entre estas fracciones, podemos distinguir como las más famosas las dos siguientes: 355/113 o 22/7.

Como curiosidad especial, comentaré que el la Bíblia aparece un error de cálculo que tiene que ver con el número π. En un relato de el libro de los Reyes, al narrarse la construcción del Palacio de Salomón, dice así :

1 Reyes 7, 23 ss :

Hizo el Mar de metal fundido que tenía diez codos de borde a borde ; era enteramente redondo, y de cinco codos de altura ; un cordón de treinta codos medía su contorno...

Lo cual es enteramente imposible, ya que si el diámetro era de 10 codos de largo, el perímetro de la circunferencia serían 10π, que es, aproximadamente, algo más de 31 codos. El error está en que el que relataba la historia sabía mucho de Religión pero poco de Geometría, y obviamente desconocía la existencia de π.

Existen multitud de artículos escritos sobre el número π. Podemos encontrar bastante información en la wikipedia. En dicho artículo encontrarás historia del número π, curiosidades, aproximaciones geométricas, fórmulas que contienen a π,...

NOTA: No olvides contrastar lo que leas en la wikipedia para asegurarte de lo que es verdad y lo que no lo es. Cualquiera puede escribir en la wikipedia y podría estar confundido.

Notas 3ºESO

Los interesados podéis ver las notas del examen del tema 5 y 6 de 3º de ESO en los siguientes enlaces:

Notas de 3º ESO A
Notas de 3º ESO B

Tema 5 de Estadísticas

La repartición del tema 5 de estadísticas queda de la siguiente forma:

Ana Benítez: Puntos 4.1 y 4.2 (hasta desviación típica incluida)
Ana Patricia: todos los modelos discretos.
Piedad: Punto 4.3 hasta la distribución exponencial incluida.
Jessica: la distribución normal.
Anabel: Distribución Chi-Cuadrado y t-Student.

Es necesario que pongáis ejemplos de todo para que se entienda mejor la asignatura.

Solución a "Conseguir uno"

Hace tiempo publiqué dos entradas ("conseguir uno" y "conseguir uno (parte dos)") donde preguntaba si erais capaces de conseguir uno quitando cinco palitos de un dibujo. Luego la cosa se complicaba intentando conseguir lo mismo pero quitando solamente cuatro palitos. Bueno, pues la solución está aquí. Supongo que casi todos lo habéis conseguido, salvo algún que otro que sigue preguntandome sobre la forma de plantear el problema.

Enhorabuena a todos los que lo habéis intentado y especialmente a los que lo habéis conseguido.

Evidentemente, las lineas discontinuas y más delgadas son las que he quitado en cada resolución.

Actualización: Evidentemente el palo central de la N está en la dirección equivocada. Un compañero me avisó del error. Gracias.

Subir nota

Ya en la primera evaluación hablamos sobre cómo se podía subir nota en la asignatura de Matemáticas. Esta entrada es para recordarlo.

El mejor método para subir nota es el de hacer alguna entrada en el blog. Para ello solo tenéis que preparar un tema que os parezca interesante y enviarme a la dirección rafa.profe@gmail.com dicha entrada. Yo la evaluaré y la publicaré en el blog. Si la entrada tiene poco interés o es demasiado sencilla os guiaré para que la mejoréis. Si al final la entrada no se puede publicar por cualquier circunstancia, no os preocupéis, que serán tomadas en consideración en la nota final igualmente.

En la primera evaluación algún compañero intentó hacer alguna entrada. Al final no se publicó, pero se vio reflejado en su nota final.

Nota Bilíngüe Tema 4

Los alumnos interesados en conocer su nota del primer examen de la segunda evaluación, loo pueden encontrar en el siguiente enlace:

Notas 1º Bilíngüe tema 4.