Inecuaciones y ecuaciones

Para que tengáis materiales con los que realizar actividades de inecuaciones que os puedan ayudar a estudiar, os dejo la siguiente relación de problemas y ejercicios resueltos.

Actividades resueltas.

El lunes podréis preguntarme dudas sobre este tema.


Para que también tengáis actividades de sistemas de ecuaciones, aquí tenéis algunos ejemplos de actividades resueltas o con la solución.

Las actividades están realizadas por otras personas de otros institutos. Agradezco su colaboración.

Evaluaciones por recuperar 4ºESO

En el archivo que se puede descargar aquí, podéis ver quién tiene que recuperar alguna de las evaluaciones del curso. Las personas que tienen una "X" junto a su nombre, tienen que recuperar esa evaluación.

El lunes se realizarán todas las evaluaciones. Yo me encargaré de que sea factible para las personas que tienen 3 evaluaciones. Ánimo y a estudiar para recuperar las evaluaciones pendientes.

P.S.: Espero agradecimientos por estar un viernes a las 2:30 de la mañana poniendo notas para que sepáis si habéis aprobado y podáis recuperar los que estéis suspensos.

Orden de exposición para el trabajo de informática

Los grupos que expondrán lo harán por este orden:

El lunes 23 de mayo, exponen el grupo 7 (Ángela y Paula) y el 12 (Ana y Mª Paz).

El miércoles 25 de mayo, exponen el grupo 13 (Águeda y Conso) y el 9 (Francisco José y Álvaro).

El viernes 27 de mayo, exponen el grupo 3 (Gonzalo y Jaime) y el 4 (Lola y Tamara).

El lunes 30 de mayo, exponen el grupo 14 (Úrsula y Carmen Rocio) y el 10 (Javier Lamprea y Alejandro Casademont).

El miércoles 1 de junio, exponen el grupo 8 (Alejandro Blanco y Javier Barrero) y el 2 (Laura y Luna).

El viernes 3 de junio, exponen el grupo 5 (Antonio y Axel) y el 6 (Iannis, Daniel Marcos y Daniel Querencio).

El lunes 6 de junio, exponen el grupo 1 (Miriam y Jenifer) y el 11 (Mª Isabel y Patricia Mª).

Recordad que puede que algún día haya una excursión o algún otro imprevisto. Las fechas por tanto pueden variar dependiendo de las circunstancias. Además es muy importante que cada grupo esté preparado para exponer el día anterior al que le toca por si alguno de los dos grupos anteriores falta ese día poder suplirlo.

P.D.: Si alguien encuentra algún error, por favor, que me avise para solucionarlo.

Juegos con palillos (respuesta)

Algunos habéis intentado contestar los juegos con palillos. Muchos habéis estado cerca. Algunos os habéis quedado muy lejos. Alguien ha acertado una de las dos. Os presento las soluciones que no se os han ocurrido:

En el primer caso, hemos quitado un palo del 9 para convertirlo en un 3, y hemos colocado ese palo sobre el 1 para convertirlo en un 7. En el segundo caso, es más complicado, quitamos un palo del 8 para convertirlo en un 6 y ese palo lo colocamos entre el 1 y el 2 para que quede 1´2 (como siempre, la coma arriba).

Muy bien a todos los que lo habéis intentado.

La historia de las cosas

Juegos con palillos

Es habitual encontrar muchos juegos de pensamiento lógico. Lo que no es tan habitual es encontrar juegos geométricos con palillos que potencien nuestro pensamiento lógico. Aquí os traigo dos ejemplos de lo que os cuento:

Os presento dos igualdades matemáticas. En la primera de ellas, que es correcta, se trata de mover un único palillo de forma que la igualdad resultante siga siendo correcta. En la segunda, incorrecta, se trata de convertirla en correcta moviendo un solo palillo.

Se aceptan contestaciones a los acertijos en los comentarios.

Si a alguien le ha gustado, podéis encontrar otros juegos con palillos aquí (os lo dejo en Open Office para que podáis modificarlo a vuestro gusto si queréis).

Frases célebres

La del matemático es una profesión extremadamente cruel. Si alguien tiene, digamos, una licenciatura en Químicas, se describirá a sí mismo como un químico. Sin embargo, si alguien lleva siendo profesor de matemáticas durante diez años y le preguntas: “¿Es usted un matemático?”, te contestará “¡Estoy intentando serlo!”

Lipman Bers

El hombre que calculaba con camellos

El siguiente texto está tomado de: Malba Tahan, El hombre que calculaba.

Hacía pocas horas que viajábamos sin interrupción, cuando nos ocurrió una aventura digna de ser referida, en la cual mi compañero Beremís puso en práctica, con gran talento, sus habilidades de eximio algebrista.
Encontramos, cerca de una antigua posada medio abandonada, tres hombres que discutían acaloradamente al lado de un lote de camellos.
Furiosos se gritaban improperios y deseaban plagas:
- ¡No puede ser!
- ¡Esto es un robo!
- ¡No acepto!
El inteligente Beremís trató de informarse de que se trataba.
- Somos hermanos –dijo el más viejo- y recibimos, como herencia, esos 35 camellos. Según la expresa voluntad de nuestro padre, debo yo recibir la mitad, mi hermano Hamed Namir una tercera parte, y Harim, el más joven, una novena parte. No sabemos sin embargo, como dividir de esa manera 35 camellos, y a cada división que uno propone protestan los otros dos, pues la mitad de 35 es 17 y medio. ¿Cómo hallar la tercera parte y la novena parte de 35, si tampoco son exactas las divisiones?
- Es muy simple –respondió el “Hombre que calculaba”-. Me encargaré de hacer con justicia esa división si me permitís que junte a los 35 camellos de la herencia, este hermoso animal que hasta aquí nos trajo en buena hora.
Traté en ese momento de intervenir en la conversación:
- ¡No puedo consentir semejante locura! ¿Cómo podríamos dar término a nuestro viaje si nos quedáramos sin nuestro camello?
- No te preocupes del resultado “bagdalí” –replicó en voz baja Beremís-. Se muy bien lo que estoy haciendo. Dame tu camello y verás, al fin, a que conclusión quiero llegar.
Fue tal la fe y la seguridad con que me habló, que no dudé más y le entregué mi hermoso "jamal1" , que inmediatamente juntó con los 35 camellos que allí estaban para ser repartidos entre los tres herederos.
- Voy, amigos míos –dijo dirigiéndose a los tres hermanos- a hacer una división exacta de los camellos, que ahora son 36.
Y volviéndose al más viejo de los hermanos, así le habló:
- Debías recibir, amigo mío, la mitad de 35, o sea 17 y medio. Recibirás en cambio la mitad de 36, o sea, 18. Nada tienes que reclamar, pues es bien claro que sales ganando con esta división.
Dirigiéndose al segundo heredero continuó:
- Tú, Hamed Namir, debías recibir un tercio de 35, o sea, 11 camellos y pico. Vas a recibir un tercio de 36, o sea 12. No podrás protestar, porque también es evidente que ganas en el cambio.
Y dijo, por fin, al más joven:
- A ti, joven Harim Namir, que según voluntad de tu padre debías recibir una novena parte de 35, o sea, 3 camellos y parte de otro, te daré una novena parte de 36, es decir, 4, y tu ganancia será también evidente, por lo cual sólo te resta agradecerme el resultado.
Luego continuó diciendo:
- Por esta ventajosa división que ha favorecido a todos vosotros, tocarán 18 camellos al primero, 12 al segundo y 4 al tercero, lo que da un resultado (18 + 12 + 4) de 34 camellos. De los 36 camellos sobran, por lo tanto, dos. Uno pertenece, como saben, a mi amigo el “bagdalí” y el otro me toca a mí, por derecho, y por haber resuelto a satisfacción de todos, el difícil problema de la herencia.
- ¡Sois inteligente, extranjero! –exclamó el más viejo de los tres hermanos-. Aceptamos vuestro reparto en la seguridad de que fue hecho con justicia y equidad.
El astuto beremís –el “Hombre que calculaba”- tomó luego posesión de uno de los más hermosos “jamales” del grupo y me dijo, entregándome por la rienda el animal que me pertenecía:
- Podrás ahora, amigo, continuar tu viaje en tu manso y seguro camello. Tengo ahora yo, uno solamente para mí.
Y continuamos nuestra jornada hacia Bagdad.

(1)Jamal, una de las muchas maneras de denominaciones que los árabes dan a los camellos.

Contesta estas preguntas:

• ¿Qué ha pasado en esta historia? ¿Crees que es justo?
• ¿Puedes expresar con números el “pico” que le sobraba al segundo hermano antes de unir el camello de Beremís? ¿y la “parte de otro” del tercer hermano?
• ¿Qué significa “eximio algebrista”?
• ¿Qué hubiese pasado si en vez de 35 camellos, fuesen 17 y Beremís hubiese actuado igual que en esta historia?

Podéis dejar vuestras contestaciones en los comentarios.

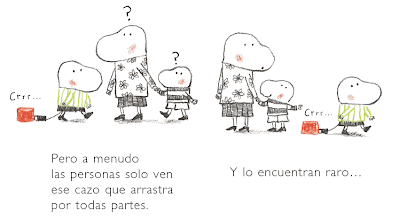
El cazo de Lorenzo

Este es un cuento infantil de la fundación FEAPS.

 

Me he permitido el lujo de completar las imágenes con el texto que las acompaña para que se muestren completamente como en el cuento. Creo que de esa forma queda mucho más bonito. Muchas gracias a María y a su amigo Santi que es el que nos lo "regaló".

 

Frases célebres

Quizás Dios no juegue a los dados con el universo, pero algo raro ocurre con los números primos.

Paul Erdos, matemático

Somos infinitamente pequeños

Durante la primera evaluación hemos hablado en clase de las potencias y de la notación científica como utilidad de las potencias. Decíamos que gracias a la notación científica, números como el billón o el trillón quedaban escritos de una manera más breve. Alguien en alguna clase me preguntó si esos números eran útiles porque... "maestro, yo nunca he usado una cantidad tan grande". Bueno, pues ahora os muestro un power point donde se utilizan esos números para hablar del universo y nos muestran cómo de pequeños (o de grandes) somos comparados con las cosas que nos rodean.

Somosinfinitamenteminusculos

View more presentations from rafaprofe.

Si alguien quiere, puede descargarse el power point "Somos infinitamente pequeños" pinchando sobre el nombre.

No a la calculadora

Como ya he comentado en muchas ocasiones la calculadora no es nuestra aliada si nos hace dependiente de ella. En los últimos días he tenido que explicarme con algunos alumnos para mostrarles por qué no permito la calculadora en clase ni en los exámenes. A ver si con un pequeño resumen queda todo más claro:

1. No tengo nada en contra de utilizar las nuevas tecnologías para facilitarnos los cálculos complejos, pero cada vez es más usual que un alumno use la calculadora para hacer operaciones básicas como 3 +7 (esto es un caso verídico que me ha ocurrido la semana pasada) Esto no se puede permitir en alumnado de ESO.
2. Existen calculadoras que son pequeños ordenadores y calculan casi cualquier operación de las que planteamos en clase, luego si el objetivo de una actividad es que el alumnado aprenda a realizar algunas actividades concretas y la calculadora lo hace por ellos, no aprende ni demuestra destreza alguna de las que se le evalúan.
3. Uno de los objetivos principales dentro del área de matemáticas es conseguir que el alumno tenga herramientas que le permitan razonar de forma clara y rápida para resolver problemas. Esto se entrena y se alcanza practicando el cálculo mental y planteando y resolviendo problemas. Con la calculadora eliminamos la posibilidad de alcanzar este objetivo.

Existen otros motivos como que para usar la calculadora hace falta entender lo que realiza la calculadora y saber que no siempre da resultados correctos (que la calculadora falla y tenemos que saber reconocer e interpretar ese fallo) pero creo que los tres motivos anteriores son los fundamentales para no permitir que uséis la calculadora.

Respuesta a 1=-1

Hace tiempo escribimos en este blog una entrada donde demostrábamos (erroneamente) que 1 es igual a -1. Todos sabemos que no es cierto, luego debíamos demostrar dónde se encontraba el fallo en la demostración. Hubo grandes jugadores que apostaron por algunos posibles errores, pero casi nadie dio con la tecla. Todos ellos han sido recompensados en las calificaciones de la primera evaluación.

Sin embargo, un participante ha usado el correo electrónico para seguir investigando hasta encontrar el error. El correo que me envió con la solución decía lo siguiente:

Quizás puede ser porque (A-B)/(A-B) sería (1-1)/(1-1) y como el paréntesis tiene prioridad, esa cuenta sería 0/0 y esa cuenta no se puede realizar.Y en la otra parte sería (-1).(A-B)/(A-B) que sería (-1).(0/0) que tampoco se podría realizar.

Francisco Pérez García.

Efectivamente el error estaba en dividir por 0. En ese caso estábamos dividiendo 0/0 que es lo que se conoce como "indeterminación". Esta operación no se puede realizar, en principio. En futuros cursos (bachilleratos) aprenderéis a trabajar con esta indeterminación.

Enhorabuena a todos los participantes porque habéis tenido grandes ideas (aunque fuesen erroneas) todas esas ideas son las que os permiten mejorar en vuestro conocimiento de matemáticas. ¡Bravo!

Soy y seré...(II)

Hace algún tiempo, desde el blog Espejo Lúdico se creó un concurso matematico-literario que me pareció divertido e interesante. Me parece que puede ser divertido recrear ese concurso a nivel escolar.

Las reglas son muy sencillas. Hay que crear una mini-historia con un máximo de 20 palabras. Pero cada palabra que uséis debe tener tantas letras como la cifra que se corresponda usando los dígitos (sin contar comas o ceros) de los números irracionales π (pi), Φ (fi) o la raíz de 2 ($ \sqrt{2} $)

π: 3´1415926535897932384
Φ: 1´6183398874989484824
$ \sqrt{2} $ : 1´4142135623739548816

Para que se entienda mejor, voy a usar un ejemplo de los que se presentaron al concurso de Espejo Lúdico. Tomando las cifras del número π, Maria del Pilar Piñones Contreras creó la siguiente frase:

Amé(3) y(1) odié(4) a(1) María(5) Gutiérrez(9): un(2) primor(6) joven(5) con(3) carne(5) preciosa(8). Fascinado(9) trituré(7) ágilmente(9) uno(3) de(2) sus(3) amorosos(8) ojos(4).

Si pincháis sobre "concurso matemático-literario" podréis ver todas las frases que se presentaron a concurso y tener otros ejemplos. Evidentemente, quien use una de estas frases para concursar estará automáticamente expulsado del concurso. Otra frase que os puede servir como ejemplo fue publicada en el blog hace justo una semana.

Evidentemente, crear una frase tan larga es sumamente difícil, pero os animo a intentarlo aunque sea con menos palabras. Podéis usar el número que os apetezca de los tres que os he escrito antes y vuestras frases deben ser enviadas a la dirección de correo electrónico: rafa.profe@gmail.com y debéis escribir en el asunto "juego números irracionales". Todos los participantes se verán reconpensados en su evaluación final y el ganador conseguirá importantes beneficios en su evaluación final de matemáticas. Mucha suerte a todos.

Sumas y restas de números enteros

Como ya informé en clase, existe por internet un juego de números enteros que creo puede ser divertido.

 Como veis en la imagen, es un juego sencillo. En donde aparecen las interrogaciones (?), cuando comencemos a jugar, aparecerán dos números enteros. Nosotros debemos escribir en la parte rosa el resultado de la operación con dichos números. Si alguien tiene alguna duda sobre cómo operar con números enteros puede pinchar en "¡Ayuda! ¡No sé hacer esto!" y se abrirá una pantalla donde te explican con ejemplos cómo operar con números enteros.

Al acabar cada partida podemos inscribir nuestros puntos en una lista con la clasificación de todos los participantes. 

Recomendación: La forma más rápida de competir es tener una mano sobre los números y otra mano sobre el signo "menos" (-) y la tecla de "Enter". Cada vez que escribes un resultado pulsas "Enter" y automáticamente aparece la nueva operación.

Mucho ánimo a todos los participantes. Los mejores serán recompensados (como siempre).

P.D.: Para que no tengáis que buscar esta entrada continuamente, he colocado la página donde se aloja el juego en los enlaces de interés que aparecen en la barra lateral del blog. La página que debemos pinchar es Dinamáticas y dentro está el "juego para aprender a operar con números enteros". 

P.D.2: Gracias a Santiago Pozo que es el creador de esta página por dejarnos usarla.

Soy y seré...

Soy y seré a todos definible,
mi nombre tengo que daros,
cociente diametral siempre inmedible
soy de los redondos aros

Clásico mnemónico de los 

primeros20 dígitos de pi 

creado por Manuel Golmayo